队列:先入先出的数据结构
本章节中,我们将首先介绍先入先出(FIFO)及其在队列中的工作方式。
本章的目的是帮助你:
- 理解 FIFO 和队列的定义;
- 能够自己实现队列;
- 熟悉内置队列结构;
- 使用队列来解决简单的问题。
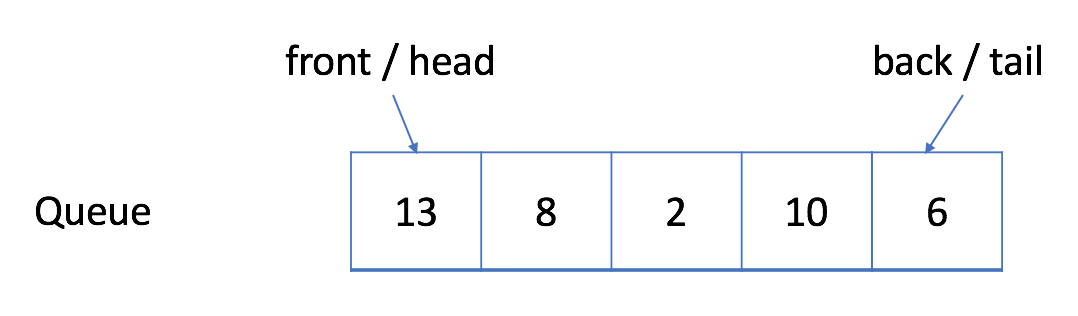
先入先出的数据结构
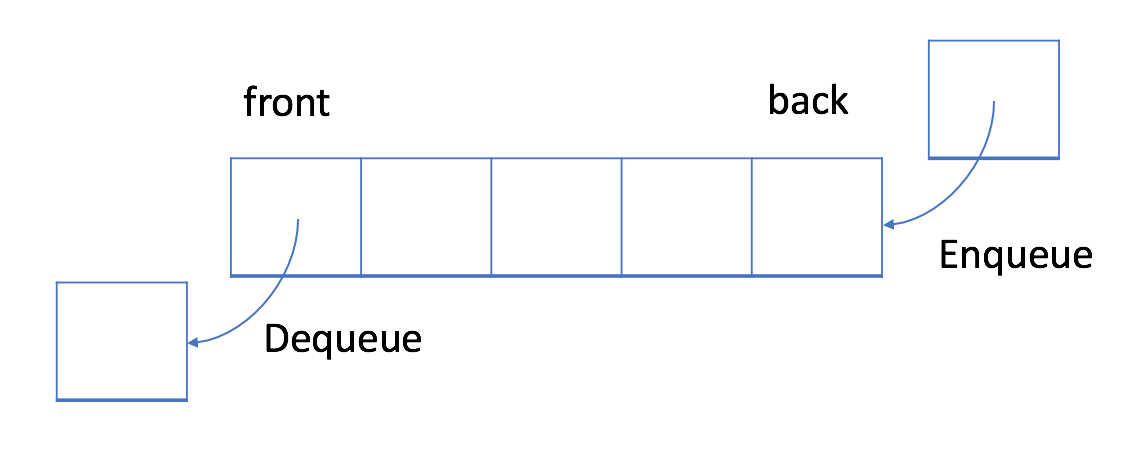
在 FIFO 数据结构中,将首先处理添加到队列中的第一个元素。
如上图所示,队列是典型的 FIFO 数据结构。插入(insert)操作也称作入队(enqueue),新元素始终被添加在队列的末尾。 删除(delete)操作也被称为出队(dequeue)。 你只能移除第一个元素。
示例 - 队列
- 入队:将新元素 6 添加到队列中。
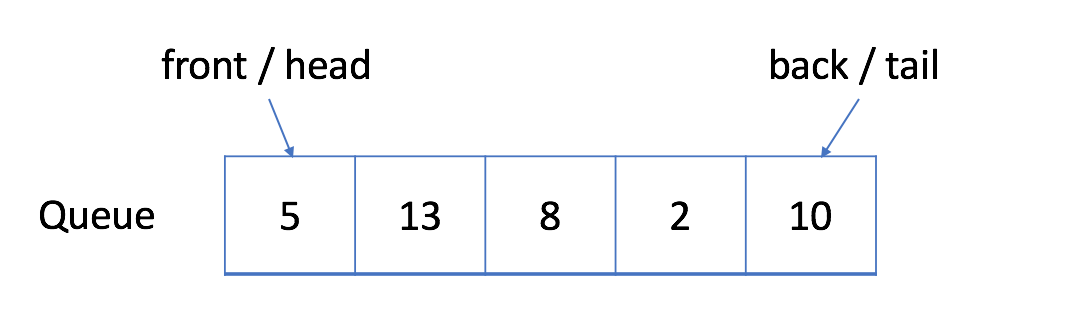
结果如下:
- 出队:将删除头元素。
结果如下:
队列 - 实现
为了实现队列,我们可以使用动态数组和指向队列头部的索引。
如上所述,队列应支持两种操作:入队和出队。入队会向队列追加一个新元素,而出队会删除第一个元素。 所以我们需要一个索引来指出起点。
这是一个供你参考的实现:
// "static void main" must be defined in a public class.
class MyQueue {
// store elements
private List<Integer> data;
// a pointer to indicate the start position
private int p_start;
public MyQueue() {
data = new ArrayList<Integer>();
p_start = 0;
}
/** Insert an element into the queue. Return true if the operation is successful. */
public boolean enQueue(int x) {
data.add(x);
return true;
};
/** Delete an element from the queue. Return true if the operation is successful. */
public boolean deQueue() {
if (isEmpty() == true) {
return false;
}
p_start++;
return true;
}
/** Get the front item from the queue. */
public int Front() {
return data.get(p_start);
}
/** Checks whether the queue is empty or not. */
public boolean isEmpty() {
return p_start >= data.size();
}
};
public class Main {
public static void main(String[] args) {
MyQueue q = new MyQueue();
q.enQueue(5);
q.enQueue(3);
if (q.isEmpty() == false) {
System.out.println(q.Front());
}
q.deQueue();
if (q.isEmpty() == false) {
System.out.println(q.Front());
}
q.deQueue();
if (q.isEmpty() == false) {
System.out.println(q.Front());
}
}
}
缺点
上面的实现很简单,但在某些情况下效率很低。 随着起始指针的移动,浪费了越来越多的空间。 当我们有空间限制时,这将是难以接受的。

让我们考虑一种情况,即我们只能分配一个最大长度为 5 的数组。当我们只添加少于 5 个元素时,我们的解决方案很有效。 例如,如果我们只调用入队函数四次后还想要将元素 10 入队,那么我们可以成功。
但是我们不能接受更多的入队请求,这是合理的,因为现在队列已经满了。但是如果我们将一个元素出队呢?

实际上,在这种情况下,我们应该能够再接受一个元素。
循环队列
此前,我们提供了一种简单但低效的队列实现。
更有效的方法是使用循环队列。 具体来说,我们可以使用固定大小的数组和两个指针来指示起始位置和结束位置。 目的是重用我们之前提到的被浪费的存储。
让我们通过一个示例来查看循环队列的工作原理。 你应该注意我们入队或出队元素时使用的策略。
设计循环队列
class MyCircularQueue {
private int[] realData;
private int head;
private int tail;
private int length;
/** Initialize your data structure here. Set the size of the queue to be k. */
public MyCircularQueue(int k) {
this.head = 0;
this.tail = 0;
this.length = k;
this.realData = new int[k];
}
/** Insert an element into the circular queue. Return true if the operation is successful. */
public boolean enQueue(int value) {
if (getCapacity() == 0) {
this.head = ++this.head;
this.tail = ++this.tail;
realData[0] = value;
return true;
}
if (getCapacity() < length) {
int result = tail + 1;
if (result <= length) {
realData[result - 1] = value;
this.tail += 1;
} else {
realData[result - length - 1] = value;
this.tail = result - length;
}
return true;
}
return false;
}
/** Delete an element from the circular queue. Return true if the operation is successful. */
public boolean deQueue() {
if (getCapacity() == 0) {
return false;
}
if (getCapacity() == 1) {
realData[this.head - 1] = 0;
this.head = 0;
this.tail = 0;
return true;
}
if (getCapacity() > 0) {
int result = head + 1;
if (result <= length) {
realData[head - 1] = 0;
this.head += 1;
} else {
realData[length - 1] = 0;
this.head = result - length;
}
return true;
}
return false;
}
/** Get the front item from the queue. */
public int Front() {
return getCapacity() == 0 ? -1 : realData[head - 1];
}
/** Get the last item from the queue. */
public int Rear() {
return getCapacity() == 0 ? -1 : realData[tail - 1];
}
/** Checks whether the circular queue is empty or not. */
public boolean isEmpty() {
return getCapacity() == 0;
}
/** Checks whether the circular queue is full or not. */
public boolean isFull() {
return getCapacity() == length;
}
private int getCapacity() {
if (tail == 0 && head == 0) {
return 0;
}
if (tail > head) {
return tail - head + 1;
} else if (tail == head){
return 1;
} else {
return realData.length - head + 1 + tail;
}
}
}
/**
* Your MyCircularQueue object will be instantiated and called as such:
* MyCircularQueue obj = new MyCircularQueue(k);
* boolean param_1 = obj.enQueue(value);
* boolean param_2 = obj.deQueue();
* int param_3 = obj.Front();
* int param_4 = obj.Rear();
* boolean param_5 = obj.isEmpty();
* boolean param_6 = obj.isFull();
*/
队列 - 用法
大多数流行语言都提供内置的队列库,因此您无需重新发明轮子。
如前所述,队列有两个重要的操作,入队 enqueue 和出队 dequeue。 此外,我们应该能够获得队列中的第一个元素,因为应该首先处理它。
下面是使用内置队列库及其常见操作的一些示例:
// "static void main" must be defined in a public class.
public class Main {
public static void main(String[] args) {
// 1. Initialize a queue.
Queue<Integer> q = new LinkedList();
// 2. Get the first element - return null if queue is empty.
System.out.println("The first element is: " + q.peek());
// 3. Push new element.
q.offer(5);
q.offer(13);
q.offer(8);
q.offer(6);
// 4. Pop an element.
q.poll();
// 5. Get the first element.
System.out.println("The first element is: " + q.peek());
// 7. Get the size of the queue.
System.out.println("The size is: " + q.size());
}
}
习题:岛屿数量
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:
11110
11010
11000
00000
输出: 1
示例 2:
输入:
11000
11000
00100
00011
输出: 3
解释: 每座岛屿只能由水平和/或竖直方向上相邻的陆地连接而成。
class Solution {
private int light = 0;
private int up = 1;
private int down = 2;
private int left = 3;
private int right = 4;
public int numIslands(char[][] grid) {
int result = 0;
// 寻找陆地
while (hasLand(grid)) {
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[i].length; j++) {
if (grid[i][j] != '0') {
result += 1;
isLand(i, j, grid, 0);
break;
}
}
}
}
return result;
}
private void isLand(int x, int y, char[][] grid, int location) {
grid[x][y] = '0';
if (location != 1 && (x + 1) <= (grid.length - 1) && grid[x + 1][y] != '0') {
isLand(x + 1, y, grid, 2);
}
if (location != 3 && (y + 1) <= (grid[x].length - 1) && grid[x][y + 1] != '0') {
isLand(x, y + 1, grid, 4);
}
if (x > 0 && location != 2 && grid[x - 1][y] != '0') {
isLand(x - 1, y, grid, 1);
}
if (y > 0 && location != 4 && grid[x][y - 1] != '0') {
isLand(x, y - 1, grid, 3);
}
}
private boolean hasLand(char[][] grid) {
for (int i = 0; i < grid.length; ++i) {
for (int j = 0; j < grid[i].length; ++j) {
if (grid[i][j] == '1') {
return true;
}
}
}
return false;
}
}
栈:后入先出的数据结构
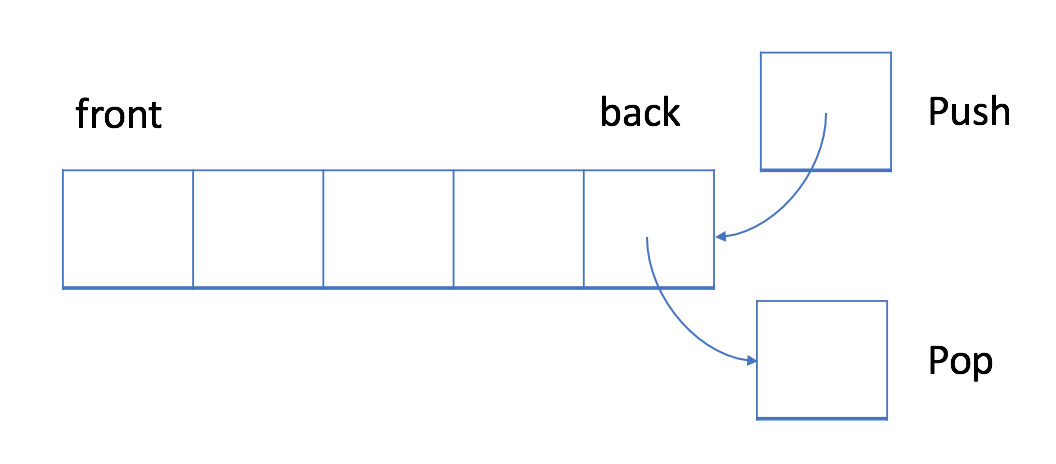
在 LIFO 数据结构中,将首先处理添加到队列中的最新元素。
与队列不同,栈是一个 LIFO 数据结构。通常,插入操作在栈中被称作入栈 push 。与队列类似,总是在堆栈的末尾添加一个新元素。但是,删除操作,退栈 pop ,将始终删除队列中相对于它的最后一个元素。
实现
// "static void main" must be defined in a public class.
class MyStack {
private List<Integer> data; // store elements
public MyStack() {
data = new ArrayList<>();
}
/** Insert an element into the stack. */
public void push(int x) {
data.add(x);
}
/** Checks whether the queue is empty or not. */
public boolean isEmpty() {
return data.isEmpty();
}
/** Get the top item from the queue. */
public int top() {
return data.get(data.size() - 1);
}
/** Delete an element from the queue. Return true if the operation is successful. */
public boolean pop() {
if (isEmpty()) {
return false;
}
data.remove(data.size() - 1);
return true;
}
};
public class Main {
public static void main(String[] args) {
MyStack s = new MyStack();
s.push(1);
s.push(2);
s.push(3);
for (int i = 0; i < 4; ++i) {
if (!s.isEmpty()) {
System.out.println(s.top());
}
System.out.println(s.pop());
}
}
}
用法
// "static void main" must be defined in a public class.
public class Main {
public static void main(String[] args) {
// 1. Initialize a stack.
Stack<Integer> s = new Stack<>();
// 2. Push new element.
s.push(5);
s.push(13);
s.push(8);
s.push(6);
// 3. Check if stack is empty.
if (s.empty() == true) {
System.out.println("Stack is empty!");
return;
}
// 4. Pop an element.
s.pop();
// 5. Get the top element.
System.out.println("The top element is: " + s.peek());
// 6. Get the size of the stack.
System.out.println("The size is: " + s.size());
}
}
习题:最小栈
public class MinStack {
private List<Integer> stack;
private Integer min;
/** initialize your data structure here. */
public MinStack() {
stack = new ArrayList<>();
}
public void push(Integer x) {
if (stack.size() == 0 && x != null) {
min = x;
}
if (x.compareTo(min) < 0) {
min = x;
}
stack.add(x);
}
public void pop() {
Integer value = stack.remove(stack.size() - 1);
if (value.equals(min)) {
for (int i = 0; i < stack.size(); i++) {
if (i == 0) {
min = stack.get(i);
}
if (min.compareTo(stack.get(i)) > 0) {
min = stack.get(i);
}
}
}
}
public int top() {
return stack.get(stack.size() - 1);
}
public int getMin() {
return min;
}
}
习题:每日温度
class Solution {
public int[] dailyTemperatures(int[] T) {
int length = T.length;
int[] result = new int[length];
Arrays.fill(result, 0);
Stack<Integer> temperatures = new Stack<>();
for (int i = length -1; i >= 0; i--) {
temperatures.push(T[i]);
}
int index = 0;
while (!temperatures.isEmpty()) {
Integer value = temperatures.pop();
int temResult = 0;
for (int i = length - temperatures.size(); i < length; i++) {
if (value < T[i]) {
temResult++;
break;
} else {
temResult++;
}
if (i == (length - 1)) {
temResult = 0;
}
}
result[index] = temResult;
index++;
}
return result;
}
}
逆波兰表达式求值
class Solution {
public int evalRPN(String[] tokens) {
if (tokens.length == 1) {
return Integer.valueOf(tokens[0]);
}
Stack<String> characters = new Stack<>();
for (int i = tokens.length - 1; i >= 0; i--) {
characters.push(tokens[i]);
}
int result = 0;
Stack<String> numbers = new Stack<>();
while (!characters.isEmpty()) {
if (!characters.peek().equals("+") && !characters.peek().equals("-")
&& !characters.peek().equals("*") && !characters.peek().equals("/")) {
numbers.push(characters.pop());
} else {
String calculate = characters.pop();
String numberOne = numbers.pop();
String numberTwo = numbers.pop();
result = calculate(calculate, Integer.valueOf(numberTwo), Integer.valueOf(numberOne));
numbers.push(String.valueOf(result));
}
}
return result;
}
private int calculate(String calculate, int a, int b) {
switch (calculate) {
case "+":
return a + b;
case "-":
return a - b;
case "*":
return a * b;
case "/":
return a / b;
}
return 0;
}
}
